שיקופים וערך מוחלט של פונקציה - חלק ג' - למורה
חומר לימוד:
השונה והמשותף בין הפעולות: שיקוף בציר \(x\), שיקוף בציר \(y\) ווערך מוחלט של גרפים ללא אסימפטוטות, למשל, כאלה שמתאימים לפולינומים. משימה זו היא משימת המשך למשימה "שיקופים וערך מוחלט של פונקציה – חלק א' וחלק ב'".
במשימה זו יש התייחסות לגרף של \(2f(x)\), כלומר נדרשת הכרות עם מתיחה אנכית של גרף של פונקציה.
כיתה:
כיתה י'
מבנה המשימה:
בעיית מטרה אחת ושתי מדרגות.
ידע קודם:
סרטוט של הפונקציות : \(|f(x)|\) , \(2f(x)\) , \(f(-x)\) , \(-f(x)\) כאשר נתון הגרף של \(f(x)\).
מטרות לימודיות:
- אפיון קשרים בין גרף של פונקציה \(f(x)\) ללא אסימפטוטות (כדוגמת פולינום) לבין הפונקציות \(|f(x)|\) , \(2f(x)\) , \(f(-x)\) , \(-f(x)\), השונה והמשותף בין פונקציות אלו.
משימת המטרה:
בבעיית המטרה נתונות חמש זהויות הקשורות לתכונות של פונקציות ו- 6 גרפים, ויש למצוא אילו גרפים מקיימים כל אחת מהזהויות הנתונות.
מדרגה 1:
במדרגה 1 ישנן שאלות המתמקדות בתכונות של פונקציות בהן עוסקת בעיית המטרה. התכונות מיוצגות בעזרת זהויות.
מדרגה 2:
במדרגה 2 תכונות של פונקציות מיוצגות בצורה מילולית ובעזרת זהויות ויש למצוא התאמה ביניהם.
שיטת הוראה:
בכיתה:
התלמידים יעבדו (רצוי בזוגות) בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה.
שימוש ביישומונים:
אין
שיעורי בית:
סיום המשימה.
משימות מומלצות:
משימות מקדימות למשימה זו:
משימה נוספת באתר בנושא זה:
בעיית מטרה
לפניכם חמש משוואות, בהן מתוארות תכונות של פונקציות – משוואות שנכונות לכל x.
קבעו עבור כל תכונה/משוואה (א-ה) באילו מהגרפים 1-6 מתוארת פונקציה שמתאימה לה.
נמקו תשובתכם. (תיתכן משוואה שמתאים לה יותר מגרף אחד, ייתכן גרף מיותר).
א. \(f(-x)=-f(x)\)
ב. \(f(-x)=f(x)\)
ג. \(|f(x)|+f(x)=0\)
ד. \(|f(x)|+f(x)=2f(x)\)
ה. \(|f(x)|=f(-x)\)
1
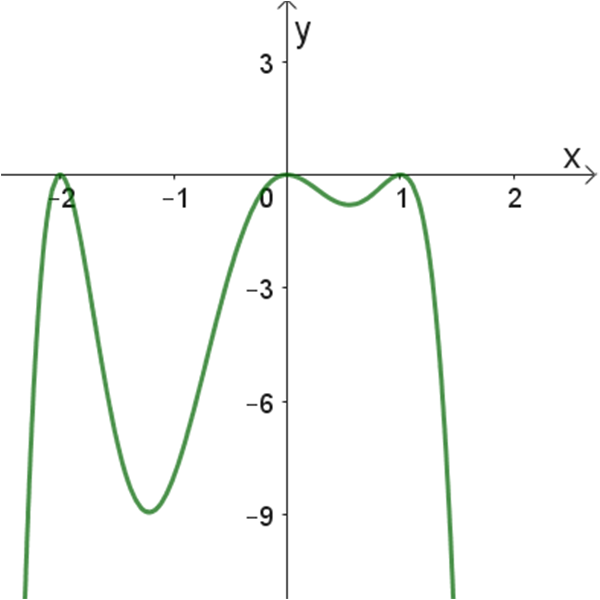
2
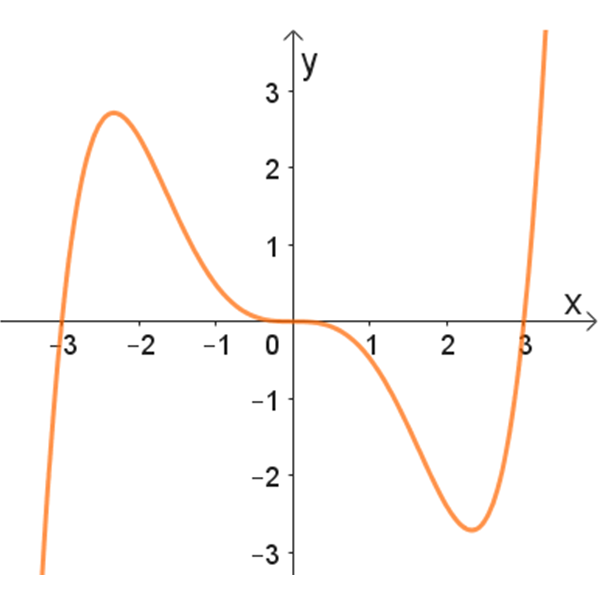
3
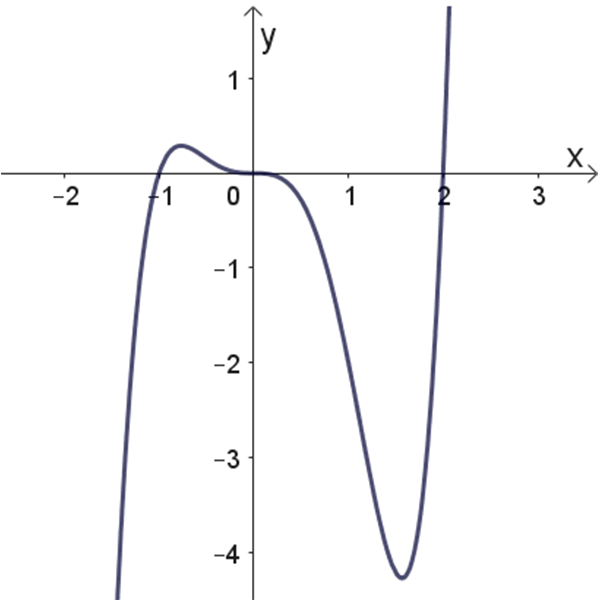
4
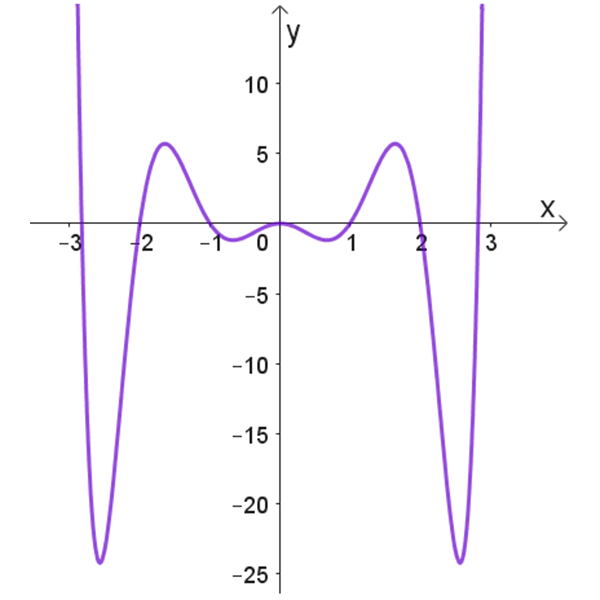
5
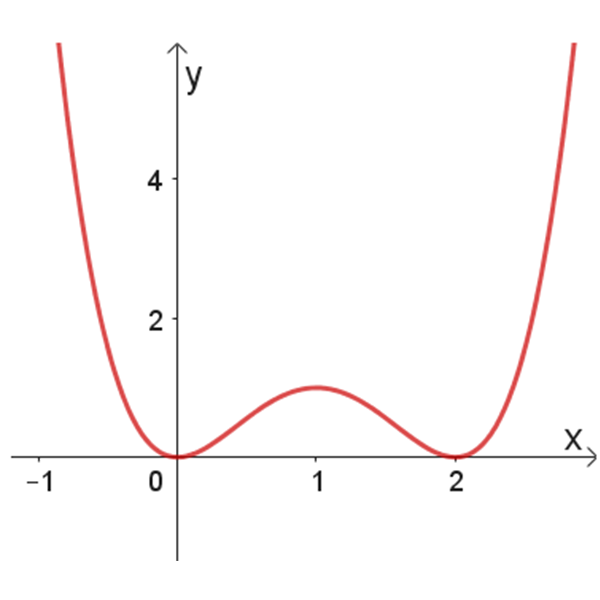
6
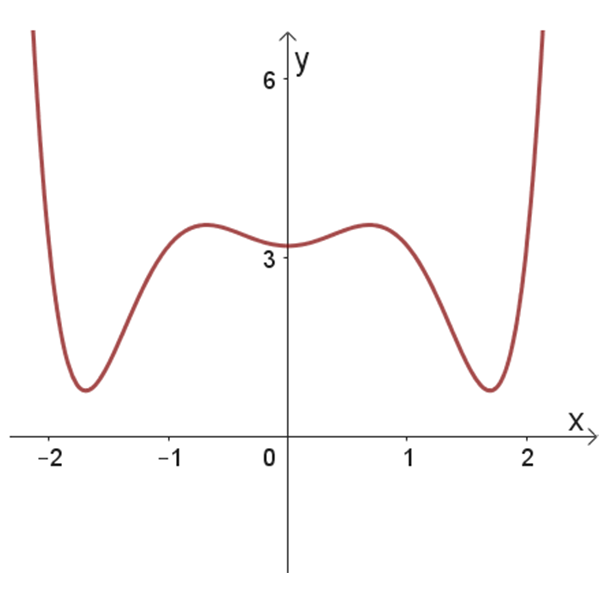
- במידת הצורך פתרו את הבעיות במדרגה 1.
פתרונות לבעיית המטרה
משוואה א
\(f(-x)=-f(x)\)
משוואה ב
\(f(-x)=f(x)\)
משוואה ג
\(|f(x)|+f(x)=0\)
משוואה ד
\(|f(x)|+f(x)=2f(x)\)
משוואה ה
\(|f(x)|=f(-x)\)
גרף: 2
גרפים: 4 ו- 6
גרף: 1
גרפים: 5 ו- 6
גרף: 6
מדרגה 1
ענו על השאלות הבאות:
סעיף א
- איזו תכונה יש לכל הפונקציות המקיימות את המשוואה הבאה לכל \(x\): \(f(-x)=-f(x)\)?
- סרטטו גרף שמתאים לפונקציה המקיימת תכונה זו. אין צורך להצביע על הביטוי המתאים לפונקציה.
סעיף ב
- איזו תכונה יש לכל הפונקציות המקיימות את המשוואה הבאה לכל \(x\): \(f(-x)=f(x)\)?
- סרטטו גרף שמתאים לפונקציה המקיימת תכונה זו. אין צורך להצביע על הביטוי המתאים לפונקציה.
סעיף ג
- איזו תכונה יש לכל הפונקציות המקיימות את המשוואה הבאה לכל \(x\): \(|f(x)|+f(x)=2f(x)\)?
- סרטטו גרף שמתאים לפונקציה המקיימת תכונה זו. אין צורך להצביע על הביטוי המתאים לפונקציה.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
מדרגה 2
נתונים הקשרים הבאים הנכונים לכל \(x\) (זהויות):
א. \(f(-x)=-f(x)\)
ב. \(f(-x)=f(x)\)
ג. \(|f(x)|+f(x)=2f(x)\)
לפניכם רשימה של תכונות של פונקציה.
לכל אחד משלושת הקשרים התאימו תכונות (אחת או יותר) שנובעות ממנו עבור פונקציה בה מתקיים הקשר:
- פונקציה שלילית בכל תחום הגדרתה
- פונקציה אי-זוגית
- פונקציה אי-שלילית בכל תחום הגדרתה
- פונקציה סימטרית סביב ציר \(y\)
- פונקציה חיובית בכל תחום הגדרתה
- פונקציה סימטרית סביב ראשית הצירים
- פונקציה זוגית
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.





















