הוכחות באמצעות שטחים - משפט תאלס - למורה
יישומונים
- – – – – –
- – – – – –
- – – – – –
- – – – – –
חומר לימוד:
הוכחת משפט תאלס באמצעות שיקולים של חישובי שטחים. המשימה מנחה להוכיח את המשפט באמצעות שיקולים של השוואת שטחים, שיטה יעילה ונדרשת בפתרון משימות הוכחה וחישוב בגיאומטריה.
משימה זו היא אחת משלוש משימות שמכוונות לשימוש בשיטה זו – המשפט בדבר נקודת מפגש התיכונים, משפט תאלס, ותכונת חוצה הזווית.
כיתה:
כיתה י'
מבנה המשימה:
בעיית מטרה, ושלוש מדרגות, בשילוב יישומון בגיאוגברה לבעיית המטרה המיועד רק לתלמידים שפותרים את בעיית המטרה, לאחר שפתרו את מדרגה 3.
ידע קודם:
- שטח משולש
- הגדרת מרחק נקודה מישר
- מרחק בין ישרים מקבילים
מטרות לימודיות:
- הוכחת משפט מרכזי בתכנית הלימודים בדרך פשוטה.
- תרגול השימוש בשיקולים של חישובי שטחים – שיקולים שנדרשים בשאלות אחרות.
משימת המטרה:
הוכחת משפט תאלס.
מדרגה 1:
בטרפז שהועברו בו האלכסונים, יש למצוא משולשים שווי שטח, ויחס בין שטחי משולשים.
מדרגה 2:
במשולש בו הועבר מקביל לאחת הצלעות יש לבטא יחס שטחים בעזרת פרמטרים.
מדרגה 3:
במשולש בו הועבר קטע המחבר קודקוד עם נקודה על הצלע שמולו, יש מצוא יחס בין שטחים.
שיטת הוראה:
בכיתה:
עבודה עצמאית או בזוגות, המעבר בין המדרגות לפי בחירת התלמיד ובהנחית המורה.
כל התלמידים יתמודדו עם הוכחת המשפט המופיע בתכנית הלימודים.
שימוש ביישומונים:
רק לתלמידים שפותרים את בעיית המטרה, לאחר שפתרו את מדרגה 3.
שיעורי בית:
תלמידים שלא סיימו לפתור את בעיית המטרה בכיתה, יסיימו את המשימה כשיעורי בית.
הערה:
בעבר היתה נהוגה הוכחת המשפט באמצעות קטעים בעלי מידה משותפת וללא שימוש בשטחים. אז הוכח משפט תאלס רק לקטעים בעלי מידה משותפת ולא ניתן היה להרחיבו לקטעים שאינם כאלה, אלא באמצעות שיקולי גבולות.
ההוכחה באמצעות שטחים עוקפת את הצורך בשימוש במושג "מידה משותפת", אך, כמובן, בדיוק כמוה מוכיחה את המשפט, לקטעים שהיחס ביניהם הוא אי-רציונאלי רק לאחר הרחבה של נוסחת חישוב שטח מלבן לאורכים אי-רציונאליים באמצעות תהליך גבולי.
משימות מומלצות:

שני מקבילים שחותכים שוקי זווית (מאותו צד של הקודקוד) מקצים על שוקי הזווית קטעים פרופוציוניים באופן הבא:
כאשר הקטע \(DE||BC\),
יש להוכיח כי: \(\Large\frac{AD}{DB}\normalsize=\Large\frac{AE}{EC}\)
- במידת הצורך, פתרו את הבעיות במדרגה 1.
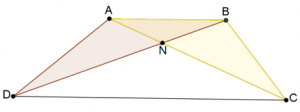
\(N\) נקודת מיפגש האלכסונים.
- מצאו בסרטוט משולשים שווי שטח.
- הוכיחו: \(\Large\frac{S_{\triangle ABN}}{S_{\triangle AND}}\normalsize=\Large\frac{S_{\triangle BCN}}{S_{\triangle DNC}}\normalsize=\Large\frac{BN}{ND}\)
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.

\(E\) נקודה על \(AC\). \(D\) נקודה על \(AB\) כך ש \(BC||DE\).
\(AE=a\) , \(EC=b\).
הביעו את היחס בין שטחי המשולשים הבאים באמצעות a ו- b:
- \(\Large\frac{S_{\triangle ADE}}{S_{\triangle CDE}}\)
\(\space\) - \(\Large\frac{S_{\triangle DEC}}{S_{\triangle DEB}}\)
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
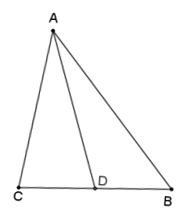
הוכיחו: התיכון לצלע במשולש מחלק את המשולש לשני משולשים שווי שטח.
סעיף ב
נתון משולש \(\triangle ABC\) , \(E\) נקודה על הצלע \(AC\).
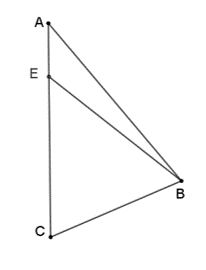
נתון: \(\Large\frac{AE}{EC}\normalsize=\Large\frac{1}{3}\).
מצאו את היחס בין שטח המשולש ABE לשטח המשולש CBE.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה (קיים יישומון).





















