מרכז מעגל החוסם משולש ומרכז מעגל החסום במשולש - למורה
חומר לימוד:
המיקום ההדדי בין מרכז המעגל החוסם משולש שווה שוקיים לבין מרכז מעגל החסום במשולש שווה שוקיים והקשר ביניהם במשולשים שונים.
מציאת המרחק בין מרכזי המעגלים כאשר נתונה זווית בסיס של המשולש ונתון בסיסו.
כיתה:
כיתה י"א
מבנה המשימה:
בעיית מטרה ושלוש מדרגות.
לכל אחת מהבעיות מצורף יישומון, בעזרתו התלמידים יכולים לבדוק כיצד משתנה המיקום ההדדי של מרכזי המעגלים, בהתאם לשינויים בהתאם לשינויים בזוויות הבסיס של המשולש.
ידע קודם:
- תכונות של מרכז מעגל חוסם משולש ומרכז מעגל חסום במשולש.
- הגדרת הפונקציות הטריגונומטריות
- זהויות טריגונומטריות.
- ניתן גם להיעזר במשפטי סינוס וקוסינוס.
מטרות לימודיות:
הבחנה כיצד משתנה דרך הפתרון למציאת הביטוי למרחק בין מרכזי המעגלים בהתאם לזוויות המשולש והמיקום של המרכזים.
שימוש בדוגמאות פרטיות על מנת להגיע להכללה.
משימת המטרה:
גילוי הקשר בין זוויות משולש שווה שוקיים לבין המיקום של מרכזי המעגלים.
מדרגה 1:
שאלה בה מרכז המעגל החוסם נמצא מחוץ למשולש
מדרגה 2:
שאלה בה מרכז המעגל החוסם נמצא קרוב יותר לקודקוד מאשר מרכז המעגל החסום.
מדרגה 3:
שאלה בה נדרשים התלמידים לזהות את המצבים ההדדיים וביחס למשולש של מרכזי המעגלים החוסמים והחסומים.
שיטת הוראה:
בכיתה:
התלמידים יעבדו בזוגות או כיחידים.
שימוש ביישומונים:
לכל אחת מהבעיות מצורף יישומון, בעזרתו התלמידים יכולים לבדוק את תשובותיהם.
שיעורי בית:
סיום המשימה
בעיית מטרה
המשולש \(ABC\) הוא שווה שוקיים \((AB=AC)\).
\(BC=k\), זווית הבסיס של המשולש היא \(\alpha\).
\(O\) הוא מרכז המעגל החוסם את משולש \(ABC\), \(M\) מרכז המעגל החסום במשולש \(ABC\).
- מצאו את:
א. האפשרויות השונות למיקום של שני המרכזים ביחס למשולש.
ב. האפשרויות השונות למיקום ההדדי של שני המרכזים ביחס לקודקוד הראש של המשולש. - עבור כל אחת מהאפשרויות שמצאתם מצאו מה התחום המתאים של הזווית \(\alpha\).
נמקו תשובתכם.לאחר שעניתם על סעיפים 1, 2, בדקו תשובתכם בעזרת היישומון המצורף (שימו לב ניתן לגרור את קודקודי המשולש ולבדוק את ערכי הזווית \(\alpha\)).
- עבור כל אחת מהאפשרויות שמצאתם סרטטו סרטוט מתאים ובטאו בעזרת \(k\) ו- \(\alpha\) את המרחק בין מרכז המעגל החוסם את המשולש לבין מרכז המעגל החסום בו.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- גרירת כל אחת מהנקודות הכחולות (\(B\) או \(C\)), משנה את המיקום של \(O\) ואת גודל הזווית \(\alpha\).
פתרונות לבעיית המטרה
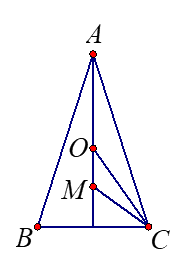
\(60^{\circ}<\alpha<90^{\circ}\)
\(OM=\Large\frac{k}{2}\normalsize[tan(2α-90^{\circ})-tan(0.5\alpha)]\)
או
\(OM=-\Large\frac{k}{2}\normalsize[tan(90^{\circ}-2\alpha)+tan(0.5\alpha)]\)
או
\(OM=\Large\frac{k}{2}[\Large\frac{-cos(1.5\alpha)}{sin(2\alpha)cos(0.5\alpha)}]\)
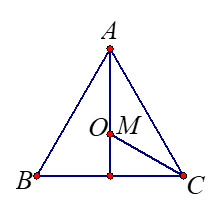
\(\alpha=60^{\circ}\)
\(OM=0\)
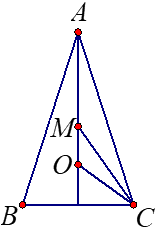
\(45^{\circ}<\alpha<60^{\circ}\)
\(OM=\Large\frac{k}{2}\normalsize[tan(0.5\alpha)-tan(2α-90^{\circ})]\)
או
\(OM=\Large\frac{k}{2}\normalsize[tan(90^{\circ}-2\alpha)+tan(0.5\alpha)]\)
או
\(OM=\Large\frac{k}{2}[\Large\frac{cos(1.5\alpha)}{sin(2\alpha)cos(0.5\alpha)}]\)
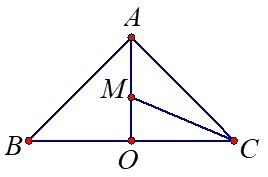
\(\alpha=45^{\circ}\)
\(OM=\Large\frac{k}{2}\normalsize tan(0.5\alpha)\)
\(OM=0.279k\)
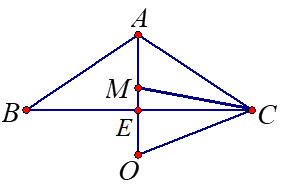
\(0^{\circ}<\alpha<45^{\circ}\)
\(OM=\Large\frac{k}{2}\normalsize[tan(90^{\circ}-2\alpha)+tan(0.5\alpha)]\)
או
\(OM=\Large\frac{k}{2}[\Large\frac{cos(1.5\alpha)}{sin(2\alpha)cos(0.5\alpha)}]\)
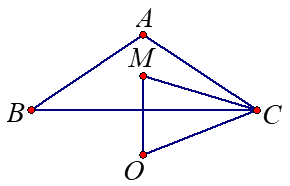
מהו התחום המתאים לזווית \(\alpha\)? נמקו תשובתכם.
בדקו תשובתכם בעזרת היישומון המצורף (שימו לב ניתן לגרור את קודקודי המשולש).
בטאו את אורכו של הקטע \(OM\) בעזרת בעזרת \(k\) ו- \(\alpha\).
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- גרירת כל אחת מהנקודות הכחולות (\(B\) או \(C\)), משנה את המיקום של \(O\) ואת גודל הזווית \(\alpha\).
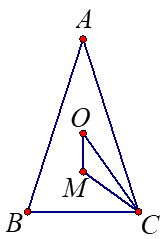
מהו התחום המתאים לזווית \(\alpha\)? נמקו תשובתכם.
בדקו תשובתכם בעזרת היישומון המצורף (שימו לב ניתן לגרור את קודקודי המשולש).
בטאו את אורכו של הקטע \(OM\) בעזרת \(k\) ו- \(\alpha\).
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- גרירת כל אחת מהנקודות הכחולות (\(B\) או \(C\)), משנה את המיקום של \(O\) ואת גודל הזווית \(\alpha\).
מדרגה 3
המשולש \(ABC\) הוא שווה שוקיים \((AB=AC)\).
\(BC=k\), זווית הבסיס של המשולש היא \(\alpha\).
\(O\) הוא מרכז המעגל החוסם את משולש \(ABC\).
\(M\) מרכז המעגל החסום במשולש \(ABC\).
לפניכם שני מצבים שונים למיקום ההדדי של שני המרכזים ביחס לקודקוד הראש של המשולש \((A)\) וביחס למשולש.
מצאו עוד שלושה מצבים אפשריים, סרטטו סרטוט מתאים.
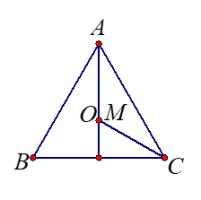

בדקו תשובותיכם בעזרת היישומון המצורף
(שימו לב ניתן לגרור את קודקודי המשולש ולבדוק את ערכי הזווית \(\alpha\))
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
- גרירת כל אחת מהנקודות הכחולות (\(B\) או \(C\)), משנה את המיקום של \(O\) ואת גודל הזווית \(\alpha\).
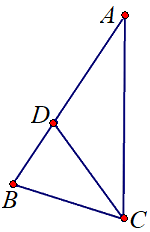
\(\measuredangle{ACB}=\alpha\) , \(CD=k\).
בטאו בעזרת \(k\) ו- \(\alpha\) את:
- רדיוס המעגל החוסם את משולש \(ABC\).
- רדיוס המעגל החסום במשולש \(ABC\).
שאלה 2
המשולש \(ABC\) הוא שווה שוקיים \((AB=AC)\).
\(O\) הוא מרכז המעגל החוסם את המשולש.
המשכו של \(OB\) חותך את \(AC\) בנקודה \(D\).
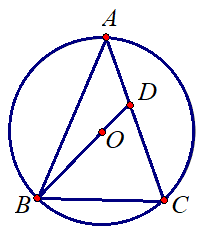
\(\measuredangle{BAC}=\alpha\) , \(BD=k\).
בטאו בעזרת \(k\) ו- \(\alpha\) את:
- רדיוס המעגל החוסם את משולש \(ABC\).
- רדיוס המעגל החסום במשולש \(ABC\).
- היחס בין רדיוס המעגל החוסם את משולש \(ABC\) לבין רדיוס המעגל החסום בו.
שאלה 3
השאלה (מלבד סעיף ד') לקוחה משאלון 806, חורף תשע"ו:
במשולש שווה שוקיים \(ABC\) \((AB=AC)\),
זווית הבסיס היא \(2\alpha\).
הנקודה \(E\) היא מפגש חוצי זוויות במשולש \(ABC\).
המשך \(CE\) חותך את הצלע \(AB\) בנקודה \(D\).
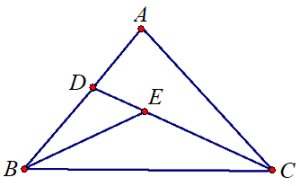
נתון: \(\frac{EC}{DE}=\frac{\sqrt{3}}{2sin{\alpha}}\) , \(\measuredangle{BAC}>90^{\circ}\)
- מצאו את \(\alpha\).
- מצאו את היחס בין רדיוס המעגל החוסם את משולש \(ABC\) ובין רדיוס המעגל החסום במשולש \(ABC\).
- נתון כי ההפרש בין רדיוס המעגל החוסם את משולש \(ABC\) ובין רדיוס המעגל החסום במשולש \(ABC\) הוא 2 ס"מ. מצאו את אורך \(AE\).
- מצאו את המרחק בין מרכז המעגל החוסם את משולש \(ABC\) לבין מרכז המעגל החסום במשולש \(ABC\).





















