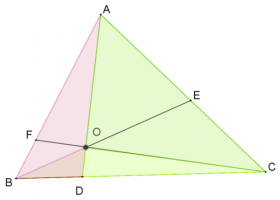
נקודת מפגש התיכונים וחותכים אחרים - הוכחות באמצעות שטחים - למורה
החומר הנלמד:
הוכחות באמצעות שטחים – ממפגש התיכונים ועד משפט צ'בה.
כיתה:
כיתה י'
אבחון המשימה:
המשימה מאגדת משפטים ותכונות שניתן להוכיח באמצעות בחינת יחס בין שטחי משולשים – מהמשפט העוסק במפגש התיכונים במשולש, דרך מפגש של חותכים אחרים דמויי תיכונים, עד להוכחת משפט צ'בה.
מבנה:
בעיית מטרה, בעיית אתגר ושלוש מדרגות.
בעיית המטרה – הוכחת משפט מכליל למשפט על נקודת מפגש התיכונים. המדרגות מאפשרות את בניית ההכללה בשלבים, ולמעשה, מציגות מקרים פרטיים בעלי משמעות עצמאית.
בעיית האתגר – הוכחת משפט צ'בה.
ידע קודם:
שטח משולש.
מטרות לימודיות:
- הוכחת משפט חשוב בתכנית הלימודים בדרך פשוטה שניתנת ליישום גם במצבים אחרים
- תרגול השימוש בשיקולים של חישובי שטחים – שיקולים שנדרשים בשאלות אחרות
- הכרות עם משפט צ'בה – המהווה הכללה למקרים פרטיים שמופיעים בשאלות שונות
- המטרה היא שכל התלמידים יתנסו בהוכחות באמצעות שטחים. רק המתקדמים יכירו את משפט צ'בה. אחרים יכולים לעצור קודם.
משימת המטרה:
הוכחת משפט מכליל למשפט על נקודת מפגש התיכונים
מדרגה 1:
מפגש חותכים דמויי תיכונים, המחלקים את הצלע ביחס 1:4.
מדרגה 2:
מפגש חותכים דמויי תיכונים, שלישונים, בצירוף הנחיה לסימון שטחים.
מדרגה 3:
מפגש תיכונים. סעיפים מפורטים לפתרון.
שיטת הוראה:
בכיתה:
עבודה עצמאית או בזוגות (רצוי בזוגות), בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה.
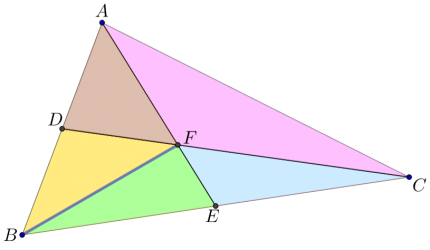
- בטאו באמצעות \(n\) את היחס בו מחלקת הנקודה \(F\) את הקטעים \(AE\) ו- \(CD\).
- הוכיחו כי הנקודה \(F\) נמצאת על התיכון מהנקודה \(B\).
- הסיקו מהנ"ל כי: שלושת התיכונים במשולש נפגשים בנקודה אחת, ונקודה זו מחלקת כל תיכון ביחס 2:1, כך שהחלק הארוך קרוב לקודקוד.
- תוכלו לעבור לבעיית האתגר.
- מידת הצורך פתרו את הבעיות במדרגה 1.
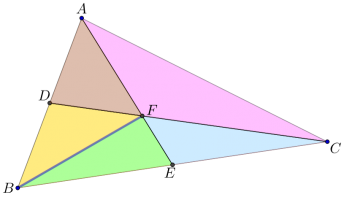
- רשמו את היחסים בין השטחים של זוגות המשולשים הבאים:
\(ABE\) ו- \(AEC\)
\(BDC\) ו- \(ADC\)
\(ADF\) ו- \(DBF\)
\(BFE\) ו- \(CFE\) - חשבו מהו היחס בין שטח המשולש \(AFC\) לבין שטח המשולש \(EFC\).
- מצאו את היחס בו מחלקת הנקודה \(F\) את הקטעים \(AE\) ו- \(CD\).
- הוכיחו כי הנקודה \(F\) נמצאת על התיכון מהנקודה \(B\).
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.

סעיף א
רשמו את היחסים בין השטחים של זוגות המשולשים הבאים:
\(ABE\) ו- \(AEC\)
\(BDC\) ו- \(ADC\)
\(ADF\) ו- \(DBF\)
\(BFE\) ו- \(CFE\)
סעיף ב
סמנו: \(S_{BDF}=S_1\) , \(S_{BFE}=S_2\)
- חשבו מהו היחס בין שטח המשולש \(AFC\) לבין שטח המשולש \(EFC\).
- מצאו את היחס בו מחלקת הנקודה \(F\) את הקטעים \(AE\) ו- \(CD\).
- הוכיחו כי הנקודה \(F\) נמצאת על התיכון מהנקודה \(B\).
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.

סעיף א
הסבירו מדוע המשולשים בכל זוג מהבאים שווים בשטחם:
\(ABE\) ו- \(AEC\)
\(ADF\) ו- \(DBF\)
\(BFE\) ו- \(CFE\)
\(BDC\) ו- \(ADC\)
סעיף ב
סמנו: \(S_{BDF}=S_1\) , \(S_{BFE}=S_2\)
- בטאו את \(S_{AFC}\) באמצעות \(S_1\)
- בטאו את \(S_{AFC}\) באמצעות \(S_2\)
סעיף ג
הוכיחו: \(AF:FE=2:1\).
סעיף ד
הסיקו את המשפט השלם בדבר מפגש התיכונים:
- נקודת המפגש של כל שני תיכונים מחלקת כל אחד מהם ביחס 2:1, כך שהחלק הארוך קרוב לקודקוד.
- בכל משולש שלושת התיכונים נפגשים בנקודה אחת.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
בעיית אתגר
משפט צ'בה (CEVA)
אם במשולש שלושה קטעים שיוצאים מהקודקודים אל הצלעות שמולם, נחתכים בנקודה אחת, אזי מכפלת היחסים שבין האורכים של הקטעים שנוצרים על כל אחת מהצלעות שווה ל-1.
כלומר: אם במשולש \(ABC\) הקטעים \(CF\) , \(BE\) , \(AD\) נחתכים בנקודה \(O\), אזי: \(\large\frac{AF}{FB}\cdot\frac{BD}{DC}\cdot\frac{CE}{EA}\normalsize=1\)