מציאת יחס חלוקה – יחידות ההצגה של ווקטורים - למורה

משימה לתלמיד

דף למורה

מבנה המשימה

יישומונים

  • – – – – –

חומר לימוד:

חישוב יחס חלוקה בין קטעים נחתכים באמצעות חשבון ווקטורים – יחידות ההצגה 

כיתה:

כיתה י"ב

מבנה המשימה:

בעיית מטרה, שלוש מדרגות ובעיית אתגר.

ידע קודם:

  • ביטוי ווקטורים באמצעות חיבור וחיסור ווקטורים נתונים
  • שימוש בפרמטר לביטוי חלק מווקטור
  • שימוש בפרמטרים לביטוי ווקטור שנמצא על מישור
  • שימוש בפרמטרים למציאת וקטור במרחב

מטרות לימודיות:  

  • תרגול השימוש בחשבון ווקטורים ובתכונת יחידות ההצגה
  • אימוץ שיטה לפתרון בעיה

משימת המטרה:

בפירמידה משולשת יש להוכיח כי הקטעים המחברים קודקוד עם מפגש התיכונים בפאה שמולו נחתכים בנקודה אחת.

מדרגה 1:

גוף מרחבי, יש למצוא באיזה יחס מחלקת נקודה וקטור נתון.

מדרגה 2:

קטעים נחתכים בטרפז, מציאת יחס החלוקה.

מדרגה 3:

תיכונים נחתכים במשולש, מציאת יחס החלוקה.

משימת אתגר:

בפירמידה ישרה שבסיסה מלבן, יש למצוא יחס חלוקה של גובה הפירמידה על ידי מישור החותך אותו.

שיטת הוראה:

בכיתה:

עבודה עצמאית או בזוגות. מעבר בין המדרגות לפי בקשת התלמידים או לפי הנחית המורה.

שימוש ביישומונים:

אין יישומונים.

שיעורי בית:

סיום המשימה.

בעיית מטרה

\(SABC\) היא פירמידה משולשת.

הנקודות \(D\) , \(E\) , \(F\) , \(G\) הן נקודות המפגש של התיכונים בפאות \(ABC\) , \(SAB\) , \(SAC\) , \(SBC\) בהתאמה.

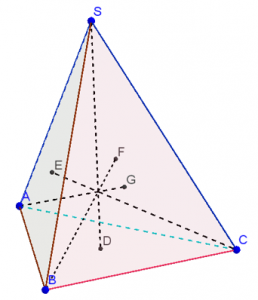
הוכיחו כי כל ארבעת הקטעים: \(SD\) , \(CE\) , \(BF\) , \(AG\) נחתכים בנקודה אחת,
ומצאו את היחס בו הם מחלקים זה את זה.

מדרגה 1

נתון טטראדר (פירמידה משולשת) \(SABC\).

שימו לב: הטטראדר הוא גוף מרחבי, על כן נוכל לבטא כל קטע בו באמצעות שלושה ווקטורים שאינם כפל בסקלר האחד של האחר.

נסמן : \(\overrightarrow{SA}=\underline{u}\) , \(\overrightarrow{SB}=\underline{v}\) , \(\overrightarrow{SC}=\underline{w}\),

הנקודה \(E\) מקיימת   \( \overrightarrow{SE}=\Large\frac{1}{9}\normalsize\underline{u}+\Large\frac{1}{12}\normalsize\underline{v}+\Large\frac{1}{18}\normalsize\underline{w}\)

המשך \(SE\) חותך את המישור \(ABC\) ב-\(F\).

נסמן: \(\overrightarrow{SF}=t\overrightarrow{SE}\) , \(\overrightarrow{AF}=l\overrightarrow{AC}+k\overrightarrow{AB}\)

1.1 הביעו את \(\overrightarrow{SF}\) בשתי דרכים.

1.2 מצאו את \(t\).

1.3 חשבו את היחס \(\Large\frac{SF}{SE}\).

  • אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
  • או, במידת הצורך, פתרו את הבעיות במדרגה 2.

מדרגה 2

בטרפז \(ABCD\), \(AD||BC\).

הקטעים \(AC\), ו-\(BE\) נחתכים בנקודה \(F\).

vectors--pic03

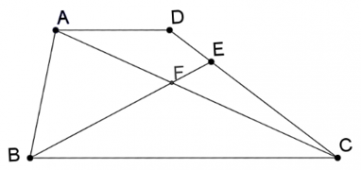
מתקיים: \(2\overrightarrow{AD}=\overrightarrow{BC}\)  ,  \(\overrightarrow{DE}=\Large\frac{1}{5}\normalsize\overrightarrow{DC}\)

נסמן: \(\overrightarrow{AD}=\underline{u}\)  ,  \(\overrightarrow{BA}=\underline{v}\)  ,  \(\overrightarrow{BF}=t\overrightarrow{BE}\)  ,  \(\overrightarrow{AF}=m\overrightarrow{AC}\)

  1. בטאו את \(\overrightarrow{AF}\) באמצעות \(\underline{u}\) , \(\underline{v}\) ו-\(m\).
    \(\space\)
  2. בטאו את \(\overrightarrow{BF}\) בשתי דרכים:
    פעם אחת באמצעות \(\underline{u}\) , \(\underline{v}\) ו-\(t\) .
    ופעם אחת באמצעות \(\underline{u}\) , \(\underline{v}\) ו-\(m\).
    \(\space\)
  3. מצאו, באמצעות חשבון ווקטורים:

1. את היחס בו מחלקת הנקודה \(F\) את הקטע \(AC\):   \(\Large\frac{AF}{FC}\) 

2. את היחס בו מחלקת הנקודה \(F\) את הקטע \(BE\):   \(\Large\frac{BF}{FE}\) 

  • אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
  • או, במידת הצורך, פתרו את הבעיות במדרגה 3.

מדרגה 3

במשולש \(\triangle ABC\), הקטעים \(AD\) ו-\(BE\) הם תיכונים.

הסבירו מדוע התיכונים בהכרח נחתכים.

vectors--pic04

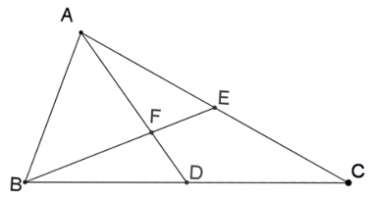
נסמן : \(\overrightarrow{AB}=\underline{u}\)  ,  \(\overrightarrow{BC}=\underline{v}\)  ,  \(\overrightarrow{BF}=t\overrightarrow{BE}\)  ,  \(\overrightarrow{AF}=m\overrightarrow{AD}\)

שימו לב: המשולש הוא גוף מישורי, על כן נוכל לבטא כל קטע בו באמצעות שני ווקטורים שאינם כפל בסקלר האחד של האחר.

  1. בטאו את \(\overrightarrow{BF}\) באמצעות \(\underline{u}\) , \(\underline{v}\) ו-\(t\).
    \(\space\)
  2. בטאו את \(\overrightarrow{AF}\) באמצעות \(\underline{u}\) , \(\underline{v}\) ו-\(m\).
    \(\space\)
  3. בטאו את \(\overrightarrow{BF}\) בשתי דרכים:
    פעם אחת באמצעות \(\underline{u}\) , \(\underline{v}\) ו-\(t\).
    ופעם אחת באמצעות \(\underline{u}\) , \(\underline{v}\) ו-\(m\).
    השוו את שתי ההצגות של \(\overrightarrow{BF}\) והסיקו את יחס החלוקה.
    \(\space\)
  4. מצאו, באמצעות חשבון ווקטורים, את יחסי החלוקה: \(\Large\frac{BF}{BE}\)  ו-\(\Large\frac{AF}{AD}\).

בעיית אתגר: מישור חותך ישר

\(ABCDE\) היא פירמידה ישרה שבסיסה הוא מלבן.

הנקודה \(G\) נמצאת על המקצוע \(ED\), כך שמתקיים: \(\overrightarrow{DG}=m\overrightarrow{DE}\).

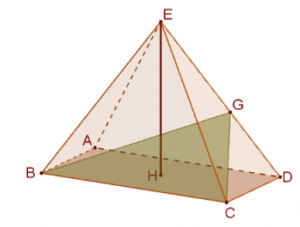
המישור שנקבע על-ידי הנקודות \(B\) , \(C\) , \(G\), חותך את גובה הפירמידה \(EH\).

\(H\) עקב הגובה במישור \(ABCD\).

נתון כי: \(\overrightarrow{AB}=\underline{u}\) , \(\overrightarrow{BC}=\underline{v}\) , \(\overrightarrow{EH}=\underline{w}\).

סמנו את נקודת החיתוך של המישור \(BCG\) עם הגובה \(EH\) ב-\(x\).

מטרתכם: למצוא את יחס החלוקה בין חלקי הגובה בהתאם לערכו של \(m\).

  1. בחרו קטע אותו תרצו לבטא בשתי דרכים שונות.
    \(\space\)
  2. הגדירו פרמטרים, ובטאו באמצעותם בשתי דרכים שונות את הקטע שבחרתם.
    \(\space\)
    תנו דעתכם: מהו הביטוי האלגברי לעובדה שהנקודה x נמצאת במישור \(BCG\)?
    \(\space\)
  3. השתמשו בהצגות השונות ומצאו את יחס החלוקה בין חלקי הגובה בהתאם לערכו של \(m\).
    \(\space\)
  4. תארו את מקומה של הנקודה x במישור.

אם התקשיתם, תוכלו להציב, למשל, \(m=\Large\frac{1}{2}\) , ולפתור את הבעיה במקרה פרטי זה.