פונקציה לוגריתמית מורכבת \(ln(f{(x)})\) - חלק ב' - למורה
חומר לימוד:
סרטוט הגרפים של הפונקציות \(ln(f^n{(x)})\) (\(n\) טבעי), כאשר נתון גרף הפונקציה \(f{(x)}\). משימת סיכום המדגישה את תכונות הפונקציה הלוגריתמית. המשימה מתאימה גם כמשימת תרגול לפני בחינת הבגרות.
כיתה:
כיתה י"ב
מבנה המשימה:
בעיית מטרה, שלוש בעיות מדרגה ובעיית אתגר. לכל אחת מהבעיות מותאמים יישומונים.
ידע קודם:
- הכרת תכונות הפונקציה \(ln(f{(x)})\)
- אפיון קשרים בין גרף של פונקציה \(f(x)\) לבין הגרפים של הפונקציות \(f^n{(x)}\) עבור \(n\) זוגי או \(n\) אי זוגי
- תכונות של פונקציה כמו: נקודות חיתוך עם הצירים, נקודות קיצון וסוגן, תחומי עליה וירידה, תחומי חיוביות ושליליות, נקודות פיתול, אסימפטוטות מקבילות לצירים, התנהגות פונקציה בקצה תחום הגדרה, הזזות של פונקציות.
הערה:
ניתן להקדים לפעילות זו את המשימה " פונקציה לוגריתמית מורכבת – חלק א' " העוסקת בקשרים שבין גרף של פונקציה \(f(x)\) לבין גרף הפונקציה \(ln(f{(x)})\).
מטרות לימודיות:
- אפיון קשרים בין גרף של פונקציה \(f(x)\) לבין גרף הפונקציה \(ln(f{(x)})\).
- אפיון קשרים בין גרף של פונקציה \(f(x)\) לבין גרף הפונקציה \(ln(f^2{(x)})\).
- אפיון קשרים בין גרף של פונקציה \(f(x)\) לבין גרף הפונקציה \(ln(f^3{(x)})\).
- הכללה לגבי קשרים בין גרף של פונקציה \(f(x)\)לבין גרפים של הפונקציות \(ln(f^n{(x)})\) עבור \(n\) זוגי ו-\(n\) אי זוגי.
- בדיקת הקשרים בלי הכרח להיעזר בנגזרת, כאשר הביטוי של הפונקציה \(f(x)\) לא נתון.
- דיון בשאלה עבור אילו פונקציות הנוסחה \(ln(f^n{(x)})=n\cdot{ln(f(x))}\) נכונה, לכל \(n\) טבעי.
משימת המטרה:
נתון גרף פונקציה \(f(x)\) יש לסרטט סקיצות של הגרפים \(ln(f^n{(x)})\) עבור \(n\) זוגי ו-\(n\) אי זוגי ולענות על השאלה: האם נכון לטעון כי עבור \(f(x)\) הנתונה מתקיימת זהות בין הפונקציות: \(ln(f^n{(x)})\) ו- \(n\cdot{ln(f(x))}\), לכל \(n\) טבעי?
מדרגה 1:
נתונים שני גרפים של \(h(x)\) ו-\(t(x)\), יש לסרטט את הגרפים של \(ln(h^n{(x)})\) ו-\(ln(t^n{(x)})\) עבור \(n=1,2,3\) ולענות, עבור כל פונקציה, האם הגרף שהתקבל זהה לגרף הנתון.
מדרגה 2:
הפונקציה הנתונה מוגדרת לכל \(x\) וללא אסימפטוטות. השאלות זהות לאלו שמופיעות במדרגה 1.
מדרגה 3:
נתונים 3 גרפים של \(f(x)\) , \(h(x)\) , \(t(x)\) יש למצוא אילו גרפים מבין הגרפים 1-9 הנתונים בטבלה מתאימים ל:
א. \(ln(f{(x)})\) ב. \(ln(f^2{(x)})\) ג. \(ln(h{(x)})\) ד. \(ln(h^2{(x)})\) ה. \(ln(t{(x)})\) ו. \(ln(t^2{(x)})\)
שיטת הוראה:
בכיתה:
התלמידים יעבדו בזוגות, הם ייחשפו תחילה לבעיית המטרה. תוך כדי העבודה בכיתה המורה ינחה את התלמידים להשתמש בבעיות המדרגה, בהתאם להתקדמותם, בהתאם לקשיים בהם ייתקלו במהלך עבודתם, ו/או בהתאם לבקשת התלמידים.
שימוש ביישומונים:
בכל בעיה ובכל שלב השימוש ביישומונים הוא לצורך בדיקה, לאחר שתלמיד חשב על השאלה, והגיע למסקנות הנדרשות. רצוי שתלמיד יסרטט את הגרפים המבוקשים במחברתו ורק אח"כ יסרטט אותם ביישומון ויבדוק תשובתו.
כדי לסרטט את הגרפים של \(ln(f^2{(x)})\), \(ln(f^3{(x)})\) רצוי שתלמיד יסרטט תחילה במחברתו את הפונקציות \(f^2{(x)}\), \(f^3{(x)}\)
אם תלמיד טעה / או לא ידע, שימוש ביישומונים יכול לעזור לו, אבל חשוב שתלמיד יידע לנמק את תשובותיו לאחר שנעזר ביישומון.
גם תלמידים שפתרו את המשימה במדרגה 1 או 2, רצוי שייחשפו ליישומונים הדינאמיים.
הערה:
אין צורך להיעזר בנגזרות, אלא בתכונה הבאה: הפונקציה \(ln(x)\) היא פונקציה עולה, לכן בתחום בו \(f(x)\) עולה ו-\(ln(f{(x)})\) מוגדרת, גם \(ln(f{(x)})\) עולה, ובתחום בו \(f(x)\) יורדת ו-\(ln(f{(x)})\) מוגדרת, גם \(ln(f{(x)})\) יורדת.
שיעורי בית:
סיום המשימה. כל תלמיד ייעזר בבעיות המדרגה בהתאם לצרכיו.
משימות מומלצות:
בעיית מטרה
בסרטוט שלפניכם נתון גרף הפונקציה \(f(x)\).
סעיף א
- סרטטו סקיצה של הגרפים ממשפחת הפונקציות: \(ln(f^n{(x)})\), עבור \(n\) אי זוגי. נמקו תשובתכם.
- כמה נקודות חיתוך יש לפונקציות ממשפחה זו עם ציר ה-\(x\)?
סעיף ב
- סרטטו סקיצה של הגרפים ממשפחת הפונקציות\(ln(f^n{(x)})\), עבור \(n\) זוגי. נמקו תשובתכם.
- כמה נקודות חיתוך יש לפונקציות ממשפחה זו עם ציר ה-\(x\)?
סעיף ג
האם נכון לטעון כי עבור \(f(x)\) הנתונה מתקיים ש: \(ln(f^n{(x)})=n\cdot {ln(f(x))}\), לכל \(n\) טבעי? נמקו תשובתכם.
תוכלו להיעזר ביישומון המצורף.
\(f(x)\)
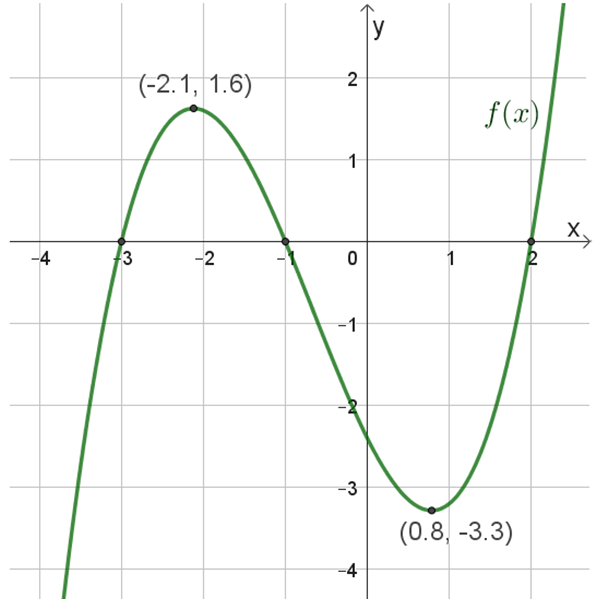
נקודות החיתוך של הפונקציה עם הצירים הן: \((2 ,0)\) , \((-1 ,0)\) , \((-3 ,0)\) , \((0 ,-2.4)\)
נקודות הקיצון: מקסימום \((-2.1 ,1.6)\) , מינימום \((0.8 ,-3.3)\)
- תוכלו לעבור לבעיית האתגר.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- יש לבחור את הפונקציה המתאימה ביישומון, ע"י בחירה של הערך \(m\) בסרגל הגרירה.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות מלאות במקומות המתאימים להן ואת הנקודות הריקות (אם יש צורך, סימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מלאות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- לשינוי המעריך (החזקה) של הפונקציה הלוגריתמית, ניתן לשנות את הערך של \(m\) בסרגל הגרירה.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ 
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
שבפינה הימנית העליונה.
פתרונות לבעיית המטרה
ג. עבור \(n\) אי זוגי, הטענה נכונה. עבור \(n\) זוגי, הטענה אינה נכונה.
\(h(x)\)
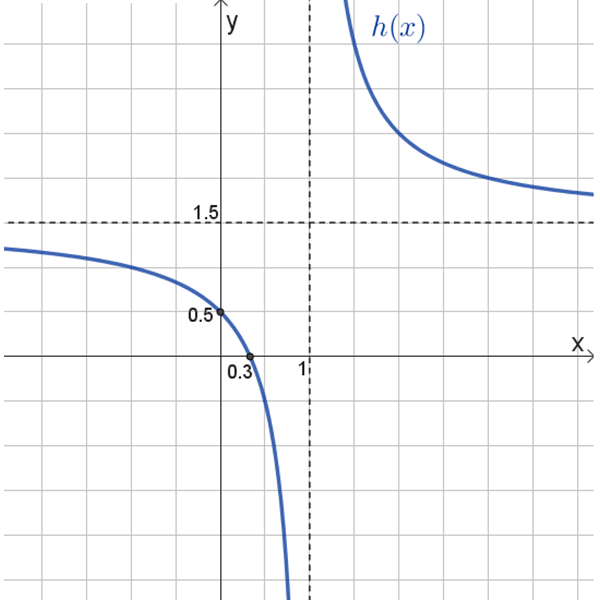
נקודות חיתוך עם הצירים: \((0.3 ,0)\) , \((0 ,0.5)\)
אסימפטוטות: \(x=1\) , \(y=1.5\)
סעיף ב
בסרטוט שלפניכם נתון גרף הפונקציה \(t(x)\).
- סרטטו את הגרפים של הפונקציות: \(ln(t{(x)})\) , \(ln(t^2{(x)})\) , \(ln(t^3{(x)})\) במערכות צירים נפרדות. נמקו תשובתכם.
- האם נכון לטעון כי עבור \(t(x)\) הנתונה מתקיים ש: \(ln(t^n{(x)})=n\cdot{ln(t(x))}\), לכל \(n\) טבעי? נמקו תשובתכם.
תוכלו להיעזר ביישומון המצורף.
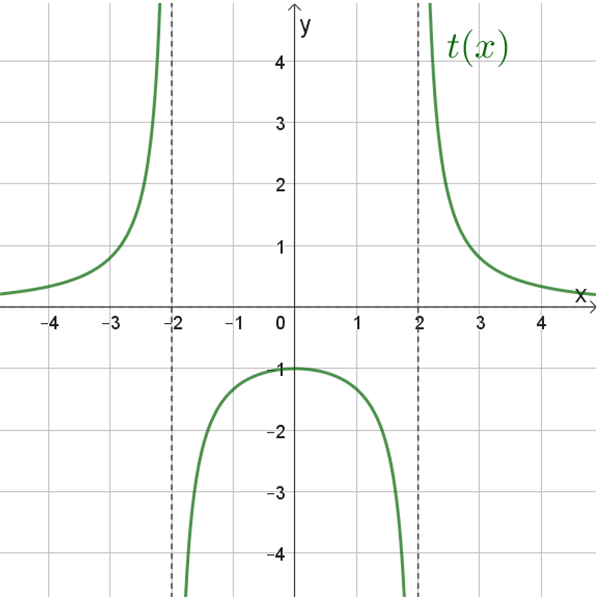
\(t(x)\)
הפונקציה חותכת את ציר ה-\(y\) בנקודה: \((0,0.6)\)
נקודת מינימום: \((1,0.5)\)
אסימפטוטות: \(x=-2\) , \(y=1\)
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- יש לבחור את הפונקציה המתאימה ביישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות מלאות במקומות המתאימים להן ואת הנקודות הריקות (אם יש צורך, סימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מלאות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- כדי לעבור לפונקציה הלוגריתמית הבאה, יש ללחוץ על החץ בתיבה הכחולה שיופיע בסיום סרטוט תקין.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
מדרגה 2
בסרטוט שלפניכם נתון גרף הפונקציה \(p(x)\).
- סרטטו את הגרפים של הפונקציות: \(ln(p{(x)})\) , \(ln(p^2{(x)})\) , \(ln(p^3{(x)})\) במערכות צירים נפרדות. נמקו תשובתכם.
- האם נכון לטעון כי עבור \(p(x)\) הנתונה מתקיים ש: \(ln(p^n{(x)})=n\cdot{ln(p(x))}\), לכל \(n\) טבעי? נמקו תשובתכם.
תוכלו להיעזר ביישומון המצורף.
\(p(x)\)
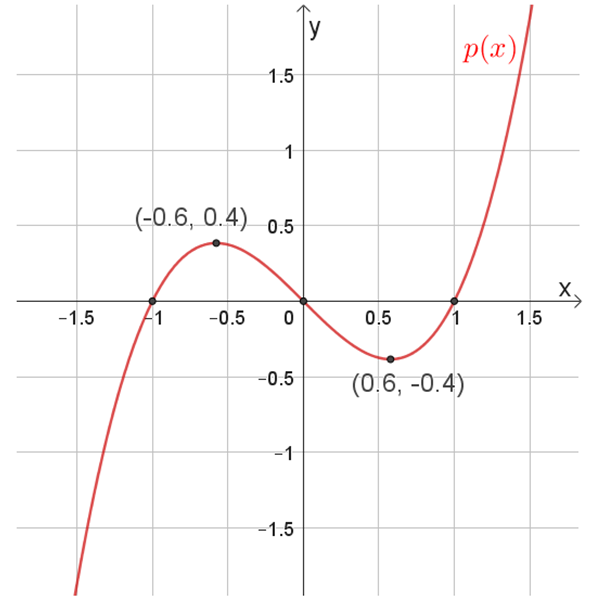
נקודות החיתוך עם הצירים: \((1,0)\) , \((0,0)\) , \((-1,0)\)
נקודות קיצון: מקסימום \((-0.6,0.4)\) , מינימום \((0.6,-0.4)\)
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- יש לבחור את הפונקציה המתאימה ביישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות מלאות במקומות המתאימים להן ואת הנקודות הריקות (אם יש צורך, סימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מלאות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- כדי לעבור לפונקציה הלוגריתמית הבאה, יש ללחוץ על החץ בתיבה הכחולה שיופיע בסיום סרטוט תקין.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
מדרגה 3
נתונים 3 גרפים של \(f(x)\) , \(h(x)\) , \(t(x)\)
- מצאו אילו גרפים מבין הגרפים 1-9 הנתונים בטבלה מתאימים ל:
א. \(ln(f{(x)})\) ב. \(ln(f^2{(x)})\) ג. \(ln(h{(x)})\)
ד. \(ln(h^2{(x)})\) ה. \(ln(t{(x)})\) ו. \(ln(t^2{(x)})\) - האם קיימות שתי פונקציות מבין הפונקציות א-ו שהן פונקציות זהות? נמקו תשובתכם.
תוכלו להיעזר ביישומון המצורף.
גרפים של פונקציות נתונות:
\(h(x)\)
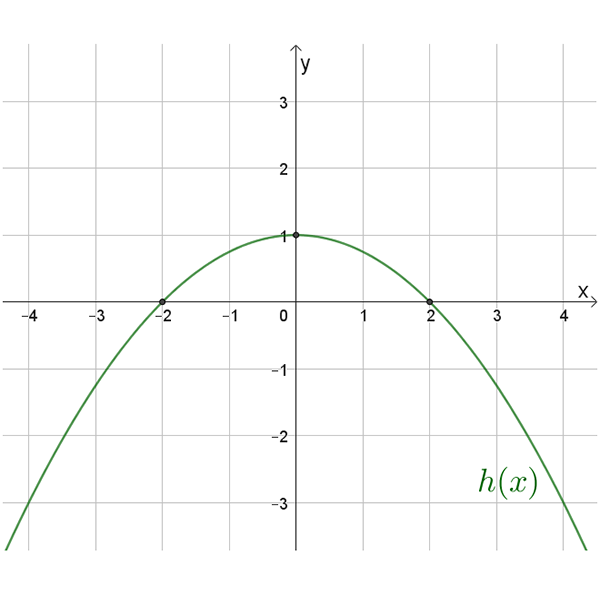
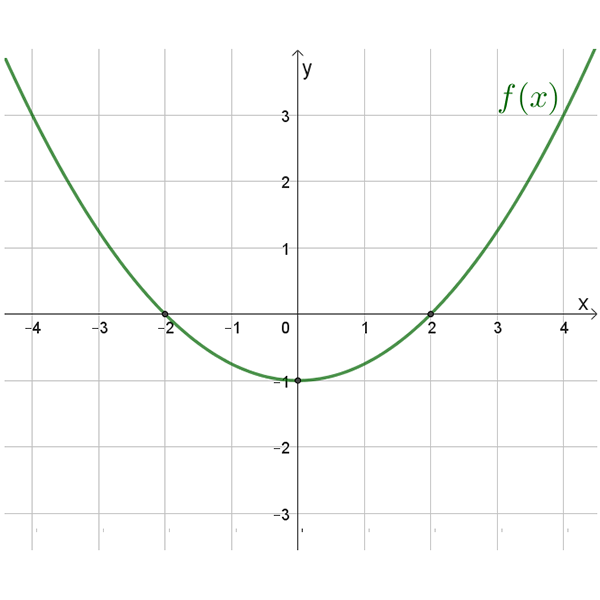
\(f(x)\)
\(t(x)\)
גרפים של פונקציות לוגריתמיות:
1
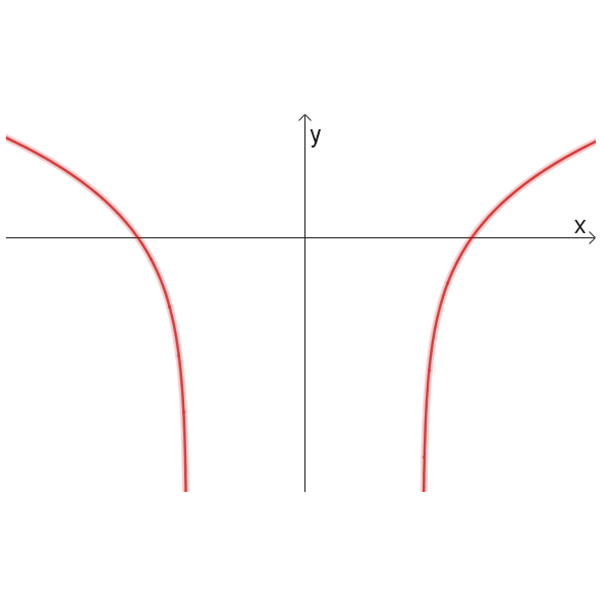
2
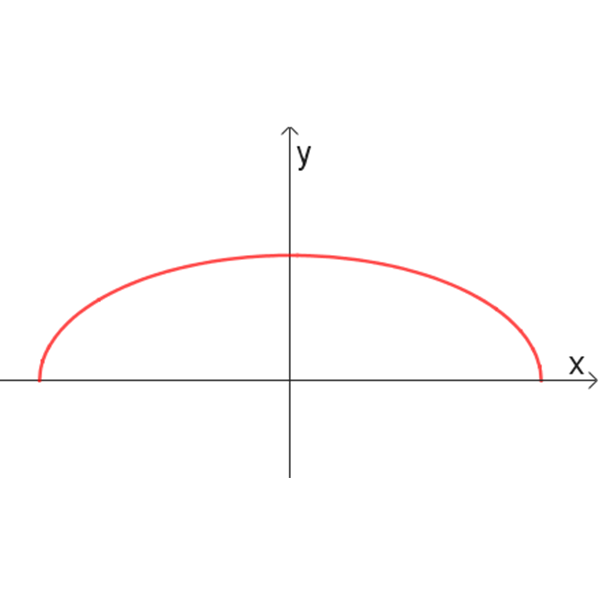
3
4
5
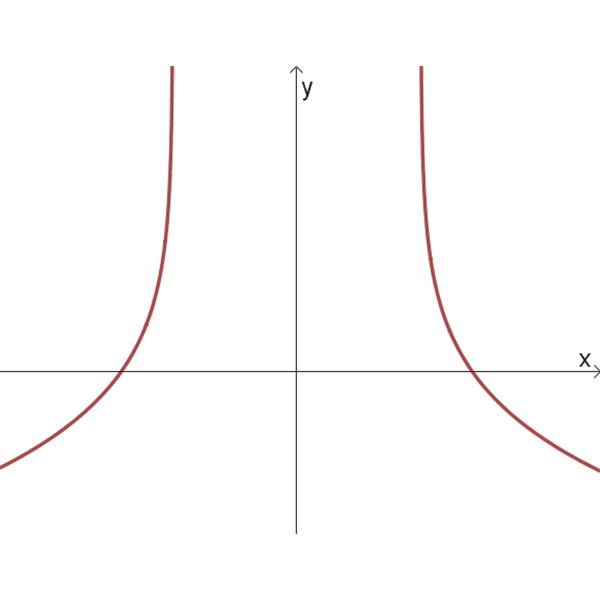
6
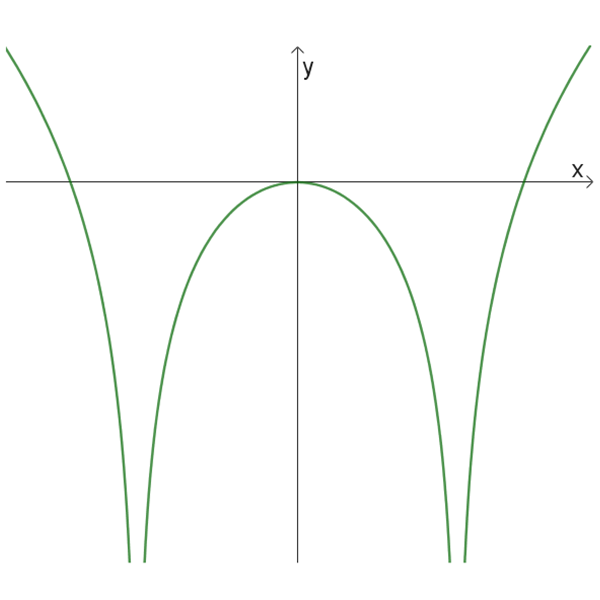
7
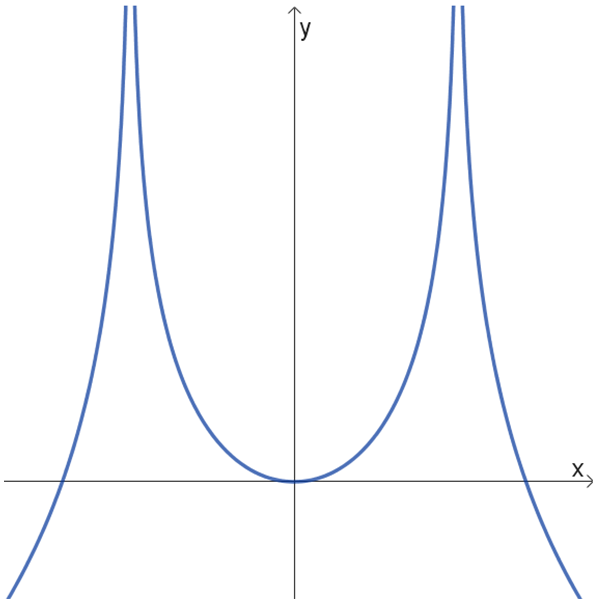
8
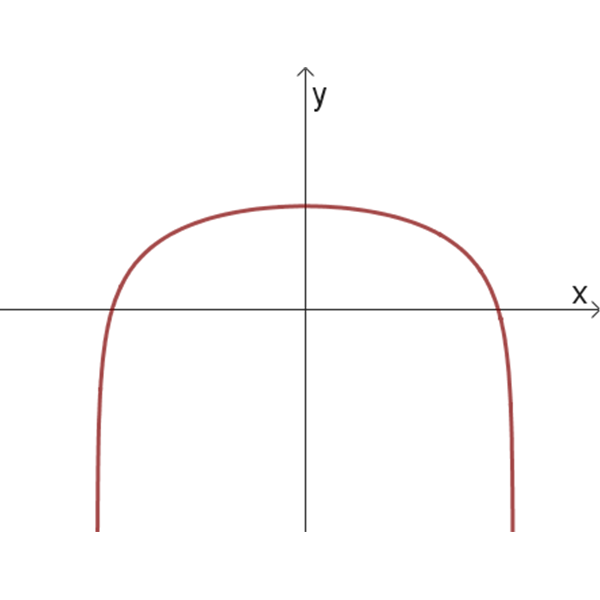
9
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
כדי להציג פרבולה, בחרו את \(h(x)\):
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה האדומה.
- ניתן למתוח את הפרבולה ואף להפוך אותה בעזרת גרירת הנקודה הכחולה, על מנת להחליף בין \(h(x)\) ו-\(f(x)\)
- לשינוי המעריך (החזקה) של הפונקציה הלוגריתמית, ניתן לשנות את הערך של \(m\) בסרגל הגרירה.
כדי להציג היפרבולה, בחרו את \(t(x)\):
- לא ניתן להזיז את הפונקציה.
- לשינוי המעריך (החזקה) של הפונקציה הלוגריתמית, ניתן לשנות את הערך של \(m\) בסרגל הגרירה.
בעיית אתגר
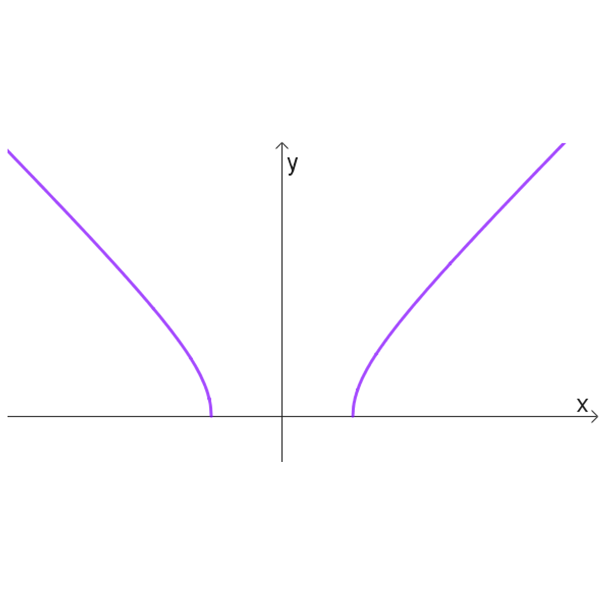
בסרטוט נתון גרף הפונקציה \(f(x)\).
- סרטטו באותה מערכת צירים בצבעים שונים את:
\(ln(f{(x)})\) , \(ln(f^2{(x)})\) , \(ln(f^3{(x)})\) , \(ln(f^4{(x)})\).
נמקו תשובותיכם.
תוכלו לבדוק תשובותיכם בעזרת היישומון המצורף. - האם נכון לטעון כי עבור \(f(x)\) הנתונה מתקיים ש: \(ln(f^n{(x)})=n\cdot {ln(f(x))}\) לכל \(n\) טבעי?
נמקו תשובתכם.
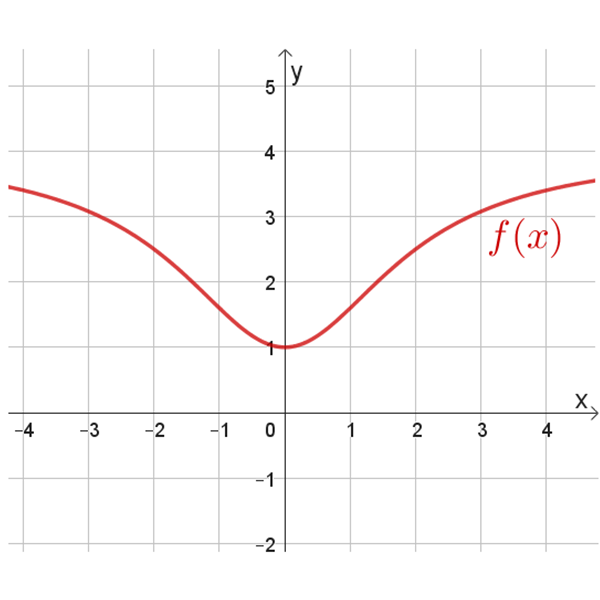
תחום הגדרה: כל \(x\)
נקודות החיתוך עם הצירים: \((0,1)\)
נקודת מינימום: \((0,1)\)
אסימפטוטה אופקית: \(y=4\)
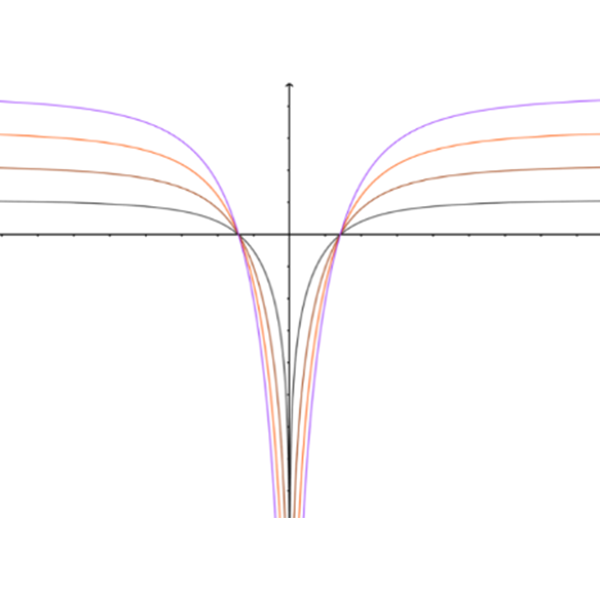
- נתון כי: \(h(x)=f(x)-k\)
בכל אחד מהסרטוטים למטה נתונים הגרפים של: \(ln(h{(x)})\) , \(ln(h^2{(x)})\) , \(ln(h^3{(x)})\) , \(ln(h^4{(x)})\) עבור \(k\) מסוים.
מצאו מה יכולים להיות ערכי הפרמטר \(k\) בכל אחד מהסרטוטים.
נמקו תשובותיכם.
תוכלו לבדוק תשובתכם בעזרת היישומון המצורף.
א
ב
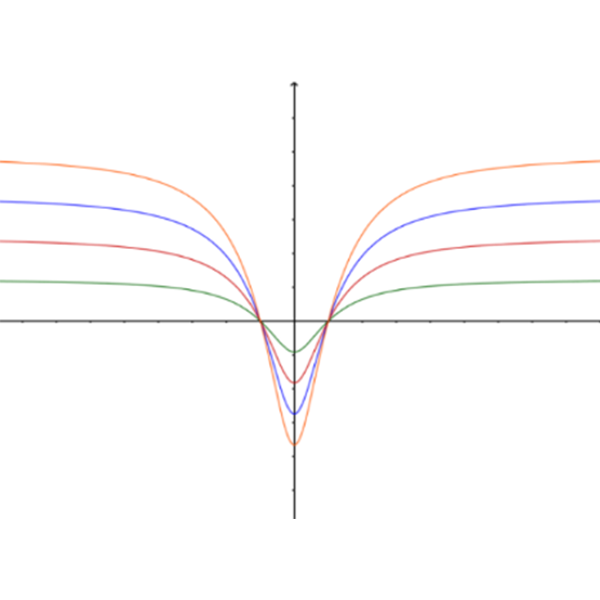
סעיף א
- לשינוי המעריך (החזקה) של הפונקציה הלוגריתמית, ניתן לשנות את הערך של \(n\) בסרגל הגרירה.
- בלחיצת מקש ימני בעכבר, כשהעכבר ממוקם על הגרף של \(ln(f{(x)})\) שמופיע ביישומון, יפתח תפריט:
- לחיצה בתפריט על Trace on ואח"כ שינוי הערכים של \(n\) יגרמו לכך שניתן יהיה לראות את אוסף הפונקציות המתקבלות: \(ln(f{(x)})\) , \(ln(f^2{(x)})\) , \(ln(f^3{(x)})\) , \(ln(f^4{(x)})\).
סעיף ב
- לצורך ניקוי המסך יש להיעזר בחיצי האתחול או בחץ undo
שבפינה הימנית העליונה שבתפריט. - יש לקבוע תחילה את \(k\) בסרגל הגרירה, ואח"כ לשנות את \(n\) בסרגל הגרירה ולבדוק אם התמונה המתקבלת היא זו המבוקשת.
פתרונות לבעיית אתגר
ב. נכון
ג. עבור סרטוט א' (מימין): \(k=1\), עבור סרטוט ב' (משמאל): \(0<k<1\)